Sistem persamaan linear dua variabel dapat diselesaikan dengan berberapa cara berikut:
1. Metode grafik yaitu dengan cara mencari titik potong dari kedua persamaan yang dibuat grafiknya. Perhatikan contoh kasus berikut!
Dalam sebuah konser musik, terjual karcis kelas I dan
kelas II sebanyak 500 lembar. Harga karcis kelas I adalah Rp 8.000,00,
sedangkan harga karcis kelas II adalah Rp 6.000,00. Jika hasil penjualan
seluruh karcis adalah Rp 3.250.000,00, tentukan banyak karcis
masing-masing kelas I dan kelas II yang terjual.
Langkah pertama adalah mengubah kalimat-kalimat pada soal cerita di atas menjadi model matematika, sehingga membentuk sistem persamaan linear. Misalkan banyak karcis I dan II yang terjual secara berturut-turut adalah x dan y, maka kalimat “Dalam sebuah konser musik, terjual karcis kelas I dan kelas II sebanyak 500 lembar,” dapat dimodelkan menjadi,
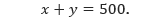
Sedangkan kalimat, “Harga karcis kelas I adalah Rp 8.000,00, sedangkan harga karcis kelas II adalah Rp 6.000,00. Jika hasil penjualan seluruh karcis adalah Rp 3.250.000,00,” dapat dimodelkan menjadi,
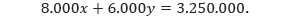
Sehingga diperoleh SPLDV sebagai berikut.
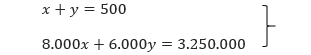
Langkah kedua, kita cari koordinat dua titik yang dilewati oleh grafik masing-masing persamaan tersebut. Biasanya, dua titik yang dipilih tersebut merupakan titik potong grafik persamaan-persamaan tersebut dengan sumbu-x dan sumbu-y.
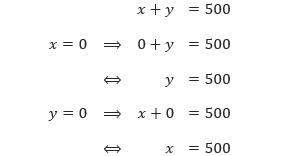
Sehingga grafik persamaan x + y = 500 memotong sumbu-x di (500, 0) dan memotong sumbu-y di (0, 500).
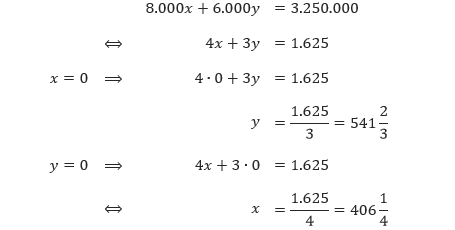
Sedangkan grafik 8.000x + 6.000y = 3.250.000 memotong sumbu-x di (406 1/4, 0) dan memotong sumbu-y di (0, 541 2/3).
Langkah ketiga, kita gambarkan grafik persamaan-persamaan tersebut pada koordinat Cartesius. Grafik persamaan-persamaan di atas dapat dilukis dengan memplot titik-titik yang telah kita cari pada koordinat Cartesius kemudian hubungkan titik (500, 0) dan (0, 500) untuk mendapatkan grafik x + y = 500, serta titik (406 1/4, 0) dan (0, 541 2/3) untuk mendapatkan grafik 8.000x + 6.000y = 3.250.000.
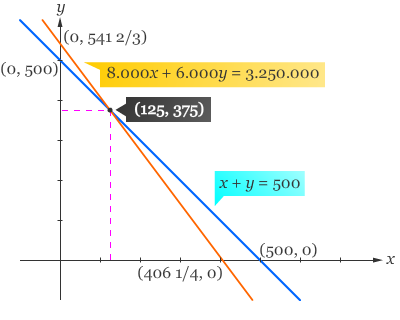
Langkah keempat, kita gunakan selesaian di atas untuk menjawab pertanyaan pada soal cerita. Karena x dan y secara berturut-turut menyatakan banyak karcis I dan II yang terjual, maka banyaknya karcis kelas I yang terjual adalah 125 lembar dan 375 lembar untuk karcil kelas II. .
2. Metode subtitusi
Contoh kasus:
Langkah pertama, kita modelkan informasi yang ada di soal menjadi persamaan-persamaan matematika. Misalkan s dan a secara berturut-turut merupakan banyaknya uang Samuel dan Andini. Karena selisih uang Samuel dan Andini adalah Rp 3.000,00, maka kalimat tersebut dapat diubah menjadi persamaan sebagai berikut.Selisih uang Samuel dan Andini adalah Rp 3.000,00. Jika 2 kali uang Samuel ditambah dengan 3 kali uang Andini adalah Rp 66.000,00. Tentukanlah besarnya uang masing-masing.

Selain itu, jumlah dari dua kali uang Samuel dan tiga kali uang Andini adalah Rp 66.000,00, maka
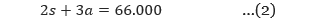
Sehingga, pada langkah pertama ini kita menghasilkan persamaan 1 dan 2 yang masing-masing dinyatakan dalam variabel s dan a.
Langkah kedua, kita akan menyatakan variabel s pada persamaan 1 ke dalam variabel a.
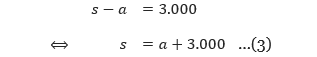
Langkah ketiga, substitusikan persamaan 3 ke dalam persamaan 2 untuk mendapatkan nilai dari a.
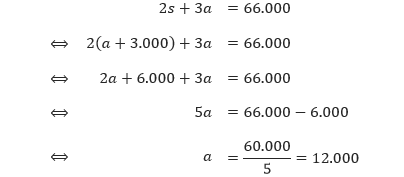
Langkah keempat, tentukan nilai variabel s dengan mensubstitusi nilai a yang diperoleh ke dalam persamaan 3.
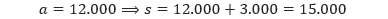
Langkah kelima, tentukan selesaian dari SPLDV yang diberikan dan jawablah pertanyaan yang diberikan soal. Dari langkah 4 dan 5, kita memperoleh selesaian dari SPLDV tersebut adalah s = 15.000 dan a = 12.000. Sehingga, banyaknya uang Samuel adalah Rp 15.000,00 dan banyaknya uang Andini adalah Rp 12.000,00.
Agar lebih jelas,silakan tonton video berikut ini!
3. Metode eliminasi
Selain dengan menggunakan metode grafik dan substitusi, permasalahan sistem persamaan linear dua variabel (SPLDV) juga dapat diselesaikan dengan menggunakan metode eliminasi. Dengan menggunakan metode ini, kita harus mengeliminasi/menghilangkan salah satu variabel dengan cara penjumlahan ataupun pengurangan. Untuk lebih jelasnya perhatikan contoh berikut.
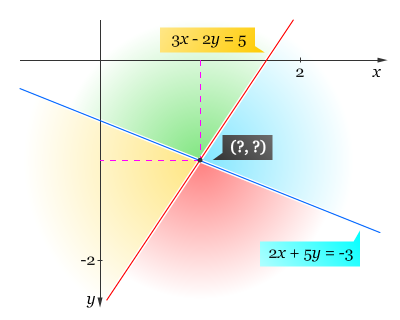
Grafik dari kedua persamaan tersebut dapat digambarkan sebagai berikut.Tentukan himpunan selesaian dari SPLDV yang memuat persamaan-persamaan 2x + 5y = –3 dan 3x – 2y = 5.
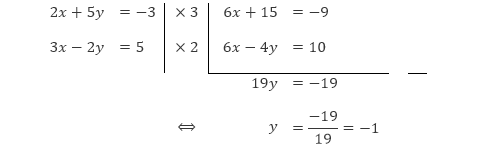
Dengan cara yang sama, kita dapat mengeliminasi variabel y untuk mendapatkan nilai dari x.
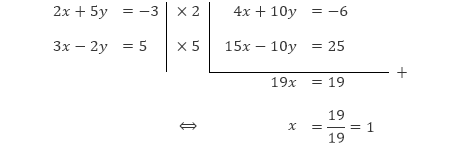
Sehingga diperoleh selesaiannya adalah x = 1 dan y = –1, atau dapat dituliskan sebagai himpunan selesaian Hp = {(1, –1)}.
4. Metode eliminasi-subtitusi
Metode eliminasi juga dapat dipadukan dengan metode substitusi dalam menyelesaikan suatu permasalahan SPLDV. Perhatikan contoh berikut.
Misalkan umur ayah dan anak perempuannya secara berturut-turut adalah m dan n, maka permasalahan di atas dapat dimodelkan sebagai berikut.Selisih umur seorang ayah dan anak perempuannya adalah 26 tahun, sedangkan lima tahun yang lalu jumlah umur keduanya 34 tahun. Hitunglah umur ayah dan anak perempuannya dua tahun yang akan datang?
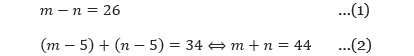
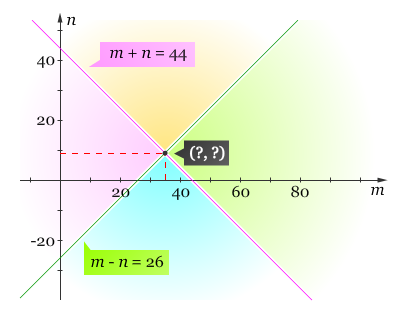
Grafik dari persamaan-persamaan m – n = 26 dan m + n = 44 dapat digambarkan seperti berikut.
Pertama, kita akan mengeliminasi variabel n untuk mendapatkan nilai dari m dengan menjumlahkan persamaan 1 dengan persamaan 2.
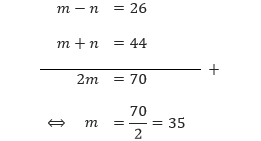
Selanjutnya kita substitusikan m = 35 ke salah satu persamaan, misalkan ke persamaan 1. Sehingga diperoleh,
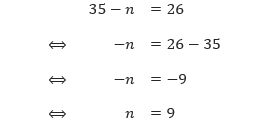
Jadi, umur ayah dan anak perempuannya saat ini secara berturut-turut adalah 35 tahun dan 9 tahun.
5. Metode determinan (menggunakan matriks). Pada pembahasan kali ini kita tidak akan menggunakan metode ini.
SEMOGA BERMAFAAT!
Tidak ada komentar:
Posting Komentar